
|
BRHS /
Borghi-diagram and interpretation of combustion regimesDepending on the ratio between the burning velocity and the flame thickness of the combustion zone, if a flame were to establish itself in a laminar flow of combustibles, and the velocity and length scales of the turbulent flow, there exist various modes of flame propagation. A flame may propagate as a reacting surface containing small scale wrinkles (wrinkled flame), as a surface containing large scale wrinkles (corrugated flame), the flame zone may be disrupted into an assembly of pockets containing reactants only, combustion products only, or a mixture of both (distributed reaction zones), or, it may be smeared out in space (well-stirred reactor regime). Each of these combustion regimes is known to have a specific burning velocity and flame thickness dependence on turbulence. 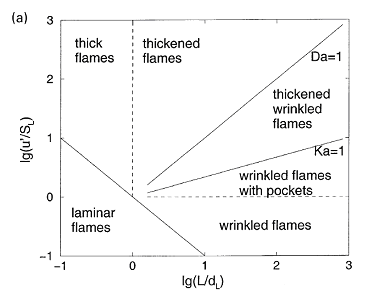 Figure 1. Borghi diagram of different combustion regimes The existence of different combustion regimes can be understood by considering the interaction between the turbulence scales and the instantaneous flame front, and with the aid of certain dimensionless groups that appear in the dimensionless form of the governing equations. A turbulent flow field is perceived to consist of a range of differently sized eddies with the macro structure and the micro structure as extremes. The eddies that form the macro structure are generated by the main flow. The Reynolds number associated with these eddies is so large that the effect of the molecular friction term in the momentum equation becomes negligible. As a consequence, the macro structure has an unstable nature (i.e. the character of the momentum equation is largely determined by the nonlinear convection term, and the large eddies ceaselessly break up into smaller ones. During this process of eddy break up the loss of kinetic energy due to viscous dissipation may be neglected. Each time a large eddy falls apart, its kinetic energy is carried on by the newly formed smaller eddies. The transfer of kinetic energy from larger to smaller eddies continues down to the micro structure, where the eddies are so small that molecular friction plays a significant role in the momentum and energy balance and the character of the momentum equation is dominated by the viscous term. Due to the consequential stability of the micro structure, the kinetic energy is no longer conveyed to smaller scales by the process eddy break up. Instead, the micro eddies convert their kinetic energy into heat. The described combustion regimes can be schematically represented on the 'turbulence intensityvs.turbulence length scale' diagram. Such diagram is used to call 'Borghi diagram' due to the name of the author who first introduced it. The lower left corner of the diagram is reserved for laminar flames. Although the precise value of Re is known to depend on the geometry of the flow domain (e.g. Re = 2000 in case of a tube; Re = 500 for the flow between two flat plates; Re = 0.1 for the flow around a spherical object), the boundary of this region is set at Re = 1. Due to the absence of turbulence scales, a flame stretch is the only interaction between the flow and the combustion. Among the remaining four regimes, the wrinkled and corrugated flames belong to the flamelet regime, which is characterised by Re > 1 (i.e. turbulence), Da > 1 (i.e. fast chemistry) and Ka < 1 (i.e. weak flame stretch). When Da > 1, and this condition covers the entire region of the distributed reaction zones as well, the time scale of the macro structure is large in comparison with the chemical time scale. This means that (i) the macro structure is not rapid enough to destroy the laminar flame structure to such a degree that the laminar burning velocity becomes an irrelevant parameter, and (ii) the chemistry is so fast that every change in the flame shape due to the large eddies is being reflected in the turbulent burning rate as the flame propagates normal to itself. Conversely, if the chemical time scale is smaller than the turbulence time scale, the flame may have changed its shape many times before any significant amount of reactants has been consumed. The flamelet regime is subdivided by a dashed line (u'/SL, u' - fluctuations velocity, SL - laminar flame speed) which forms the boundary between the wrinkled and corrugated flame sheets. Clearly, if u' < SL and u' is interpreted as the rotation speed of the largest eddies, even these cannot fold the flame. The turbulence merely wrinkles the flame front (see Figure 3.4), and the turbulent burning velocity is largely determined by laminar flame propagation. In spite of the weak influence of the flow field, the average flame thickness will be greater than in the laminar case. The turbulent burning velocity associated with this flame regime can be described by Karlovitz’s result for large scale, low intensity turbulence (which is Damkohler’s equation). In the corrugated flame regime, u'< SL < uK, and the flame front will be pushed around and folded by the largest eddies. The smallest eddies which are just capable of affecting the flame are those with a rotation velocity equal to the laminar burning velocity, and their size is known as the Gibson scale. When Ka = 1, the Gibson scale is equal to the Kolmogorov scale, LG = LK, which means that even the smallest eddies of the flow field are capable of wrinkling the laminar flame surface. The distributed reaction zone regime starts at the line Ka = 1. When Ka approaches unity, and this starts to occur in the wrinkled flame regime, the laminar burning velocity is modified by flame stretch. If Ka = 1, the macro eddies will fold the flame front to form bulges of a size in the order of Lt while the micro scale eddies distort the flame surface into bulges of a size in the the order of LK. If these bulges extend into the unburnt mixture, their radius of curvature is negative, and the local laminar burning velocity becomes less than that of an unstretched flame. At the small bulges the radius of curvature is so small (i.e. the effect of flame quenching due to curvature is so large) that local extinction occurs. The flame is cut into pieces by the small eddies, and these pieces are scattered across the flame zone by the larger eddies. As a consequence there is no well defined flame structure, and the flame front consists of a collection of pockets of unburnt and burnt mixture. In spite of the fact that the laminar flame structure is being disrupted by the turbulence in this combustion regime, the condition Da > 1 indicates that the laminar burning velocity remains a relevant parameter: the local consumption of reactants within a pocket occurs at a rate which is determined by the local laminar burning velocity at its boundary. The overall consumption rate of reactants, however, is determined by the instantaneous interfacial area between the unburnt and burnt mixture. A well known model that is used to describe the average volumetric fuel consumption rate in this combustion regime with success is the so called eddy-breakup model (Spalding, 1971, Bray, 1980). This model relies on the assumption that the overall consumption rate of reactants is determined by the rate at which parcels of unburnt mixture are broken down into smaller ones, thereby increasing the interfacial area between the unburnt and burnt mixture. In the regime of the well stirred reactor, Re > 1, Da < 1 and Ka > 1. The condition Da < 1 indicates that the chemistry is slow in comparison with the turbulence. Under these circumstances the fluid elements of the burning zone are shifted so rapidly in space that no laminar flame structures can be discerned as in the case of the other combustion regimes. The burning zone rather propagates as a homogeneous reactive zone with some reaction occurring everywhere. Spalding D.B. (1971), Mixing and chemical reaction in steady confined turbulent flames. 13th Symposium (Int.) on Combustion, The Combustion Institute, Pittsburgh, 649-657. << Interaction between turbulence and flames: turbulent burning velocity | Content | Effect of obstacles on flame propagation and pressure build up >> |