
|
BRHS /
Free jet laminar and turbulent diffusion flames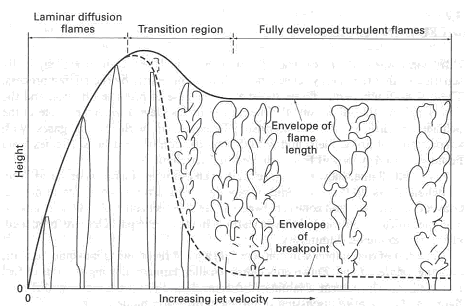 Figure 1. Free jet diffusion flame transition from laminar to turbulent flow (HottelHC:1949). Consider a gaseous fuel jet upward from a nozzle of diameter dj into stagnant air as shown in Figure 1. As the velocity of the fuel jet is increased, the character of the flame changes. At low jet velocity the mixing rate is slow and the flame is long and smooth (laminar). The laminar flame height increases linearly with jet velocity up to a point where the flame becomes turbulent. The flame height decreases due to more rapid turbulent mixing. In the stable, fully developed turbulent region, the flame height is independent of jet velocity. The transition to a fully developed turbulent flame may be characterized by a transition Reynolds number given in Table 1 (HottelHC:1949). As the jet velocity is further increased, a point is reached where the flame lifts off from the nozzle and exhibits a nonburning region at the bottom. A further increase in jet velocity causes the flame to blow off completely. Table 1. Jet diffusion flame transition to turbulent flow [Hottel and Hawthorne 1949]
In engineering practice, it is very useful to obtain quick solution by phenomenological analyses. Such simple approach gives the following dependence of the laminar diffusion jet flame height on the fuel volumetric flow rate \dot{V} and mass diffusivity D (KuoKK:2005): z_{f,L} \propto \frac{\dot{V}}{D}.
More fundamental approach gives following expressions for the flame radius at any particular z station and flame length (KuoKK:2005) r_{f} = z\frac{16}{\sqrt{3} Re_{d_{0} } } \sqrt{\sqrt{\frac{3}{16} \frac{Re_{d_{0} } r_{0} }{z f_{st} } -1} },
z_{f} = r_{0} \frac{3}{16} Re_{d_{0} } \left[ 1 + \frac{1}{ \left({F / O)_{st} Y_{O,A}} \right) } \right],
Re_{d_{0} } \equiv \frac{u_{0} d_{0} }{\nu } , f_{st} =\frac{\left(F/O\right)_{st} Y_{O,A} }{1+\left(F/O\right)_{st} Y_{O,A} },
where: r0, d0 - radius and diameter of fuel jet at the exit, respectively, u0 - fuel velocity at the exit, YO,A - mass fraction of the oxidizer in the ambient gas, (F/O)st - stoichiometric fuel to oxidizer ratio. Turbulent diffusion flame height is observed to be independent of the fuel volumetric feed rate but linearly dependent upon the nozzle diameter. Hottel H.C. and Hawthorne W.R. (1949) Diffusion in laminar flame jets. In Proceedings of the Third Symposium (International) on Combustion. Baltimore. Williams and Wilkins, pages 253-266.(BibTeX) << Jet fires in congested environment, effect of delayed ignition | Content | Triple flames >> |