
|
BRHS /
OFD-Chapter 1Chapter 1. Hydrogen fundamentalsIntroduction
General
Hydrogen is the first element in the periodic table with the atomic number 1. It is the lightest and most abundant element in the universe representing 75 mass% or 90 vol% of all matter. On Earth, it is mostly found in compounds with almost every other element. Considering just the compound water, the hydrogen contents bound in the total water supply of the world is on the order of 1014 t. Hydrogen exists also as a free element in the atmosphere, but only to the extent of less than 1 ppm (by volume). Free ionic hydrogen is more reactive than molecular hydrogen, the nonpolar-covalent compound of two hydrogen atoms. In 1776, Henry Cavendish identified hydrogen as a distinct species. It was given the name “water maker” by Antoine Lavoisier seven years later, who proved that water was composed of hydrogen and oxygen. The most common hydrogen isotope is protium (H-1, H, atomic mass 1.007822). The second isotope is the stable deuterium (H-2, D) or heavy hydrogen discovered in 1932 by H. C. Urey and co-workers. Deuterium has a natural fraction of 0.014 % with physical and chemical properties slightly different from H-1. Nearly all D in natural hydrogen is in combination with hydrogen atoms, the diatomic HD with a fraction of 0.032 % in natural hydrogen; the existence of molecular D is highly improbable. Third hydrogen isotope is the radioactive tritium (H-3, T) with a half life of 12.3 years, discovered in 1934 by E. Rutherford. But also the short-lived isotopes H-4, H-5, and H-7 have been synthesised in the meantime. Physical Properties of HydrogenHydrogen can be considered an ideal gas over a wide temperature range and even at high pressures. At standard temperature and pressure conditions, it is a colourless, odourless, tasteless, non-toxic, non-corrosive, non-metallic diatomic gas, which is in principle physiologically not dangerous. One of its most important characteristics is its low density, which makes it necessary for any practical applications to either compress the hydrogen or liquefy it. It is positively buoyant above a temperature of 22 K, i.e., over (almost) the whole temperature range of its gaseous state. Hydrogen gas is highly diffusive and highly buoyant; it rapidly mixes with the ambient air upon release. The diffusion velocity is proportional to the diffusion coefficient and varies with temperature according to Tn with n in the range of 1.72-1.8. Corresponding diffusion rates of hydrogen in air are larger by about a factor of 4 compared to those of air in air. The rising velocity under the influence of (positively) buoyant forces cannot be determined directly, since they are dependent on the density difference between hydrogen and air as well as on drag and friction forces, shape and size of the rising gas volume, and atmospheric turbulence. The positive buoyancy of hydrogen is a favourable safety feature in unconfined areas, but it can cause a hazardous situation in (partially) confined spaces, where the hydrogen can accumulate, e.g., underneath a roof. Both diffusion and buoyancy determine the rate at which the gas mixes with the ambient air. The rapid mixing of hydrogen with the air is a safety concern, since it leads very soon to flammable mixtures, which on the other hand – for the same reason – also will quickly dilute to the non-flammable range. Therefore it is estimated that in a typical unconfined hydrogen explosion, only a fraction of the gas mixture cloud is involved releasing in fact not more than a few per cent of the theoretically available energy. Because of its small size, its small molecular weight and its low viscosity, hydrogen can cause a problem with respect to the propensity of the gas to leak at a larger molecular flow rate than other gases. Diffusion in small amount is even possible through intact materials, in particular organic materials, which may lead to gas accumulation in confined spaces. Leakage rates are by a factor of 50 higher than for water and by a factor of 10 compared to nitrogen. The addition of an odorant or colorant would ease the detection of small leaks; however, this is not practicable in most situations, and not feasible for LH2. Hydrogen gas dissolved in liquids will permeate into adjoining vessel materials. At elevated temperatures and pressures, hydrogen attacks mild steels severely, causing decarburization and embrittlement. This is a serious concern in any situation involving storage or transfer of hydrogen gas under pressure. Proper material selection, e.g., special alloy steels, and technology is required to prevent embrittlement. Hydrogen coexists in two different forms, ortho and para hydrogen, whose partition is dependent on the temperature. Normal hydrogen at room temperature is 75 % ortho (nuclear spins aligned) and 25 % para (spins anti-aligned). In the lower temperature range < 80 K, para hydrogen is the more stable form. At 20 K, the thermal equilibrium concentrations are 99.821 % para and 0.179 % ortho. The transition takes place over a longer period (about 3-4 days), until a new equilibrium state is reached. However, magnetic impurities and also small oxygen concentrations are able to catalyze ortho-para conversions raising the rate by several orders of magnitude (very good: Fe(OH)3) to the order of hours. Any concentration of either spin state can be created at any temperature through the action of catalysts. Most physical properties are differing only slightly between the two spin states. Most important is the large energy difference between the two varieties, which results in major differences for the specific heats and thermal conductivities. The presence of a radiation field results in the generation of free hydrogen atoms and ions, which also act as catalysts before recombining. The recombination on the other hand produces excess ortho hydrogen. Hydrogen also exhibits a positive Thompson-Joule effect at temperatures above 193 K, the inversion temperature. It means that the temperature of the hydrogen gas increases upon depressurization, which may lead to ignition. For example, the temperature change is six degrees, if a sudden pressure drop from 20 MPa to ambient pressure takes place. The chance of a spontaneous ignition just by that effect, however, is small; an explosion is more likely to occur because of electrostatic charging of dust particles during the depressurization or autoignition at high temperatures. Liquid hydrogen (LH2) has the advantage of extreme cleanliness and the more economic type of storage, however, on the expense of a significant energy consumption of about one third of its heat of combustion. Another drawback is the unavoidable loss by boiloff which allows to maintain the cold temperature in the tank. The evaporation rate is even enhanced when ortho hydrogen is stored. The heat liberated during the ortho-para conversion at 20 K is huge with 670 kJ/kg compared to a figure of 446 kJ/kg for the latent heat of vaporization at the same temperature. This represents a safety issue requiring a design of the hydrogen loop which is able to remove the heat of conversion in a safe manner. For open LH2 pools, it needs to be considered that cold hydrogen gas is less volatile compared to ambient gas and thus more prone to the formation of a flammable mixture with air. Furthermore LH2 quickly contaminates itself due to condensation and solidification of air constituents, which can particularly lead to oxygen-enriched zones to form shock-explosive mixtures. In confined areas, an additional hazard is given by the fact that due to the volume increase by a factor of 845, when LH2 is heated up to ambient conditions, the local atmosphere may change drastically. In an enclosed space, final pressure may rise to 172 MPa, which certainly over pressurizes systems to bursting. A further temperature decrease below the boiling point eventually results in mixtures of liquid and solid hydrogen or slush hydrogen, SLH2. Slush offers the advantages of a higher density and a prolongation of the storage time of the cryogen as the solid melts and absorbs heat. A safety risk is arising from the decreasing vapour pressure even below atmospheric pressure, which demands protection against air ingress into the system. In addition, the conversion of ortho to para hydrogen connected with the release of the respective heat of conversion as the solid is form, needs to be taken into account (SonntagRE:1988). The triple point finally is the temperature (13.8 K) and pressure (7.2 kPa), at which all three phases can exist in equilibrium. If hydrogen (or any other fluid) is maintained above its critical temperature and pressure is applied, a single phase "supercritical fluid" forms. It is gas-like in that it is compressible, it is liquid-like in that it has a comparable density, and there is some transitory state in between characterized by strong structural fluctuations causing the unusual behaviour of fluid properties near their critical point. It also exhibits higher flow rates as compared with liquids. There is a strong dependence of the thermophysical properties of cryogenic hydrogen on temperature and pressure in the supercritical state. They vary strongly especially in the near-critical region. Cp has a maximum at the then called the pseudo-critical temperature ("thermal spike phenomenon"). Supercritical hydrogen might undergo a turbulent-to-laminar transition due to the dependence of viscosity on temperature. Heat transfer coefficients are unpredictable in the transition regime, and are much lower in the laminar regime. Hydrogen at extreme, but accessible pressures (2-3*105 MPa) and temperatures (~ 4400 K) will make a phase transition to metallic hydrogen which may be superconducting at room temperature. This effect predicted in 1935 was eventually proven in a shock compression test in 1996. Metallic hydrogen is accepted to exist in the interior of Saturn and Jupiter, but has no practical application on Earth so far. Hydrogen is both in the gaseous and liquid phase essentially an insulator. Only above some critical "breakdown" voltage, where ionization occurs, it becomes an electrical conductor. Invalid BibTex Entry! Chemical Properties of HydrogenHydrogen reacts both with non-metals (high electro-negativity) and with metals (low electro-negativity) to form either ionic or covalent hydrides (e.g., HCl, H2O). The electro-negativity, a measure for the attraction of electrons to the nucleus, of hydrogen is 2.20 (Pauling scale). Hydrogen is able to react chemically with most other elements. In connection with oxygen, hydrogen is highly flammable over a wide range of concentrations. As a fuel it represents a clean, environmentally benign energy source. The mass-related energy density of hydrogen is very high; 1 kg of hydrogen contains 132.5 MJ, which is approximately 2.5 times more energy than is contained in 1 kg of natural gas. The energy content of hydrogen is given as either lower heating value (LHV) of 242 kJ/mol or as higher heating value (HHV) of 286 kJ/mol. The difference of 15.6 %, which is large compared to other gases, is due to the heat liberated upon condensation of the water vapour (which could be captured in a turbine, but not in a fuel cell). A stoichiometric hydrogen-air mixture, where all fuel is consumed upon reaction, i.e., where maximum combustion energy is released, contains 29.5 vol% of hydrogen. The combustion product of hydrogen is water vapour. It burns in a non-luminous, almost invisible pale blue, hot flame to water vapour liberating the chemically bound energy as heat (gross heat of combustion). The flame temperature of a burning (premixed stoichiometric) hydrogen-air mixture is max. 2403 K. There is a wide flammability range of hydrogen (at room temperature) between 4 and 75 vol% of concentration in air and up to 95 vol% in oxygen. The lower flammability limit (LFL) as the minimum amount of fuel that supports combustion, is usually the “more important” limit, since it will be reached first in a continuous leakage. The flammability range widens with higher temperatures. The influence of the temperature is expressed in the modified Burgess-Wheeler equation for the LFL, which is for hydrogen (at ambient pressure) (ZabetakisMG:1967):
where ΔHc is the net heat of combustion and T given in [K]. The respective equation for the upper flammability limit (UFL) is (EichertH:1992):
valid for the temperature range 150-300 K. Measurements of upward flame propagation at higher temperatures (GasseA:1992) have shown a further increase of the UFL with initial temperature reaching 87.6 % at 673 K. There is still no experimental data available on the influence of moisture on the flammability limits. For the determination of LFL and UFL of mixtures of fuels, the Le Chatelier rule is the most commonly applied method:
where yi is the volume fraction and Li the flammability limit of fuel i. Le Chatelier’s rule was found to be in accurate agreement with experimental data for the system H2-CO, but shows deviations up to 35 % for the systems methane-propane or methane-ethane (SubramanyaM:2005). The GEXCON handbook states that "the formula does not work properly for H2". The potential for an explosion of a flammable hydrogen-air mixture is very high. The auto-ignition temperature, which is the minimum temperature of a hot surface that can ignite a flammable mixture, is for hydrogen in the range of 800-1000 K depending on the experimental conditions. It is relatively high, but can be lowered by catalytic surfaces. Hydrogen gas does not have a flash point as it is already a gas at ambient conditions. It means that cryogenic hydrogen will flash at all temperatures above its boiling point of 20 K. The minimum ignition energy, i.e., the spark energy required to ignite the "most easily ignitable hydrogen concentration in air" (which is usually not the stoichiometric mixture), is with 0.02 mJ very low, much lower than for hydrocarbon-air mixtures. A weak spark or the electrostatic discharge by a flow of pressurized H2 gas or by a person (~ 10 mJ) would suffice for an ignition. This is, however, no different from other burnable gases. The minimum ignition energy is further decreasing with increasing temperature, pressure, or oxygen contents. The hot air jet ignition temperature is lowest for hydrogen compared to all hydrocarbons decreasing further with increasing jet diameter. It is also dependent on jet velocity and mixture composition. The "maximum experimental safe gap" (MESG) is the maximum distance between two flat plates which still allows flame propagation through the gap; it is for hydrogen 0.08 mm. The “quenching gap” in air is the distance between two flat plates at which ignition of a flammable mixture is suppressed. It corresponds to the smallest diameter of a tube through which a flame can propagate. Faster burning gases have smaller quenching gaps. Hydrogen has a quenching gap of 0.64 mm. Because of the high explosion pressures, the MESG is always smaller than the quenching gap. 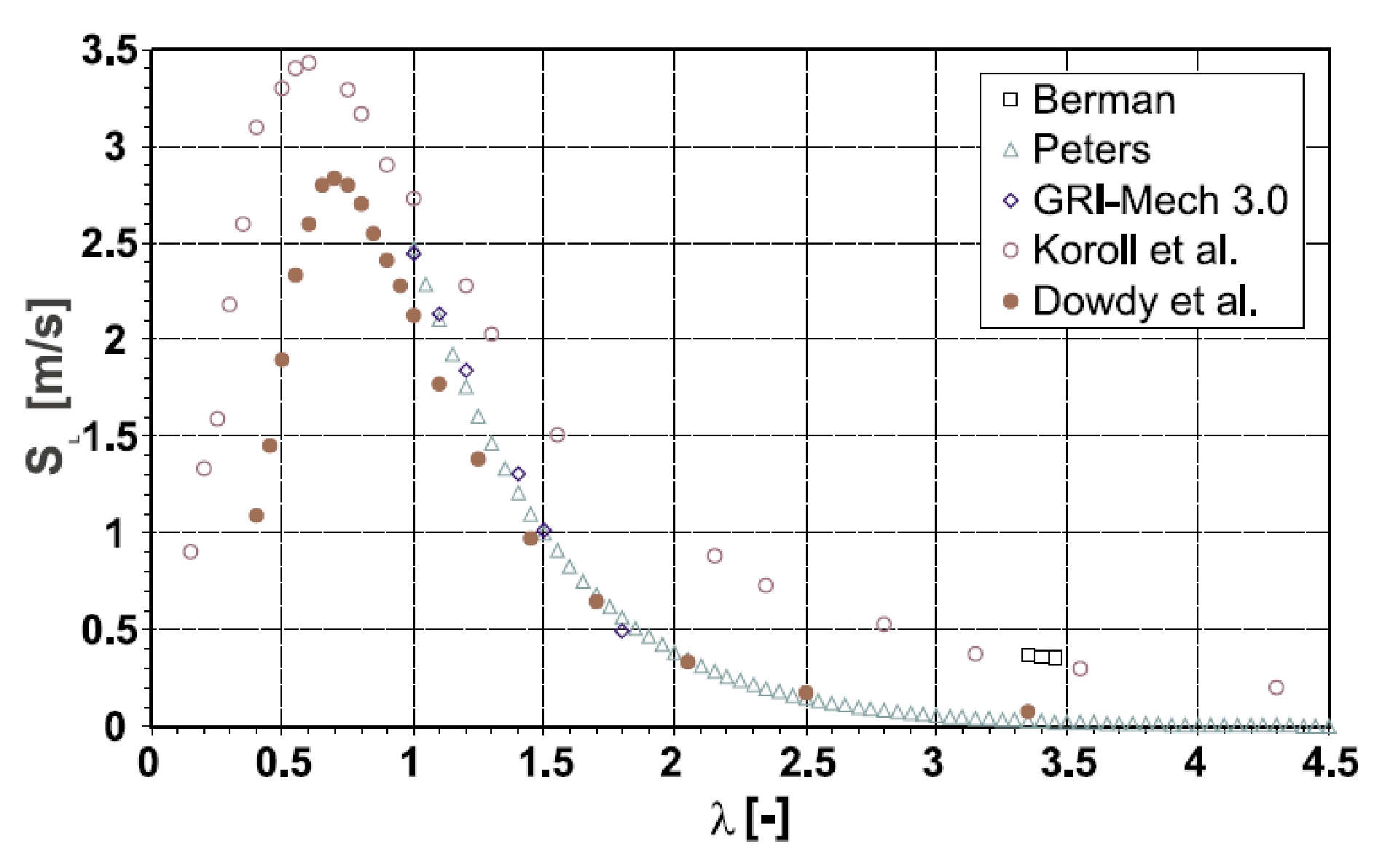 Fig. 1: Burning velocities in hydrogen-air mixtures as measured by various authors ([[http://www.hysafe.net/wiki/BRHS/OFD-Chapter1?action=bibentry&bibfile=DB&bibref=KroenerM:2002 | KroenerM:2002)]] The burning velocity in a flammable gas mixture, different from the flame speed, is indicating the speed with which a smooth plane combustion wave advances into a stationary flammable mixture and is a pertinent property of the gas depending on temperature, pressure, and concentration. The burning velocity of hydrogen in air at stoichiometric ambient conditions (Fig. 1) is 2.55 m/s reaching a maximum of 3.2 m/s at a concentration of 40.1 %, which would even increase to 11.75 m/s in pure oxygen. Compared to other hydrocarbon fuel-air mixtures, it is highest for hydrogen because of its fast chemical kinetics and high diffusivity. The higher the burning velocity, the greater is the chance for a transition from deflagration to detonation (DDT). In contrast, the flame speed, which is related to a fixed observer, is much greater than the burning velocity due to the expansion of the combustion products, instabilities, and turbulent deformation of the flame. The maximum possible speed of a deflagrative burning flame is given by the speed of sound in the combustion products gas mixture, which is 975 m/s for a stoichiometric hydrogen-air mixture. The detonability range is usually given to be 18-59 vol% of hydrogen concentration, however, the range was found to be depending on the system size. In Tieszen et al. (TieszenSR:1986), a detonation range of 13-70 % of H2 is given for a 43 cm tube. In the Russian detonation test facility RUT, the largest of its kind, a lower detonability limit of as low as 12.5 vol% has been observed. In pure oxygen, the detonation range is extended to 15-90% (ZabetakisMG:1967). The detonation velocity in air reaches values in the range of 2000 m/s; in pure oxygen, it is up to 3500 m/s. The size of the detonation cell is a measure of the reactivity; the smaller the cell, the more reactive is the mixture (Fig. 2). It serves to some extent as an indicator for DDT and can be measured experimentally. A stoichiometric hydrogen-air mixture with a cell size of 15 mm is highly reactive, whereas a stoichiometric methane-air mixture with a cell size measured of approx. 330 mm is the least sensitive of the common fuels. Cell sizes increase with increasing deviation from stoichiometry. It was in the late 1970s, when the usefulness of measurements of the detonation cell size λ was well acknowledged. First step was finding a correlation between cell size and critical tube diameter (d=13*λ). This empirical law was the basis to develop a simple surface energy model which allows the derivation of a critical initiation charge weight for various hydrocarbon-air mixtures in pretty good agreement with experimental data. The critical tube diameter is the minimum diameter required for a detonation wave to emerge from a tube and become a detonation in an unconfined cloud. It is a measure of minimum dimensions of an unconfined detonable cloud. The detonation initiation energy given in mass of high explosive (TNT or tetryl) is the minimum energy necessary to initiate a spherical detonation wave; the energy content of tetryl corresponds to 4.3 MJ/kg. The distance in which the flame front at the ignition point develops to a detonation depends on many parameters such as temperature, pressure, mixture composition, geometry (obstacles), and ignition source strength. For a stoichiometric hydrogen-air mixture to detonate, a typical figure of tube length over diameter ratio is approximately 100. It is known from the experience that a hydrogen-air gas cloud evolving from the inadvertent release of hydrogen upon the failure of a storage tank or pipeline liberates only a small portion of its thermal energy contents in case of an explosion, which is in the range of 0.1-10 %, in most cases < 1 % (LindCD:1975). 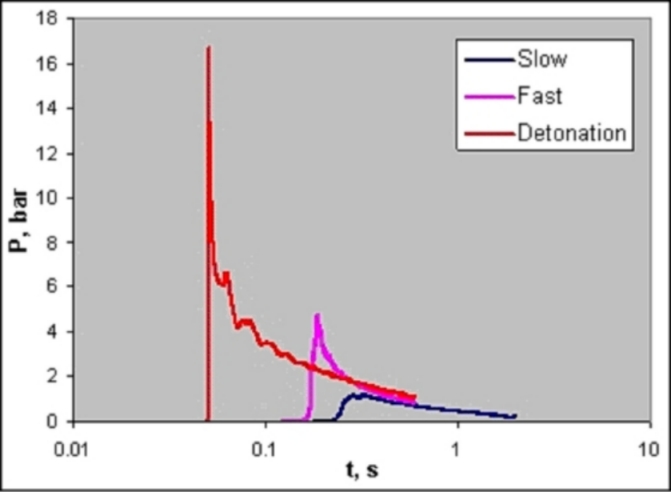 Fig. 3: Pressure signals from different hydrogen combustion modes ([[http://www.hysafe.net/wiki/BRHS/OFD-Chapter1?action=bibentry&bibfile=DB&bibref=KuznetsovM:2005 | KuznetsovM:2005)]] The explosion of a hydrogen-air mixture cloud results in the formation of a pressure wave, which is different dependent on the combustion mode as is shown in Fig. 3. In the deflagration of a free hydrogen-air gas cloud, the maximum overpressure is in the order of 10 kPa. An overpressure of 7 kPa is still deemed not dangerous; at 7 kPa, people would fall down to the ground; at 35 kPa, damage of ear drums is expected; 240 kPa is considered a threshold value above which fatalities must be taken into account. The thermal energy radiated from a flame corresponds to the higher heating value. It can be reduced due to absorption by moisture in the atmosphere. The radiation emitted from a hydrogen flame is very low due to a strong absorption by the ambient water vapour (emissivity ε < 0.1) unlike hydrocarbon flames (ε ~ 1) (ArthurDLittle:1960). Therefore, despite its high flame temperature, the burning hazard is comparatively small. The major problem is given in the non-visibility even in a dark room (unless impurities in the air are present), and therefore difficult to recognize and localize. An advantage of hydrogen-air fires is the fact that there is no smoke generation (assuming no other material be ignited), which is important for confined areas. Invalid BibTex Entry! Main Characteristic Data of Hydrogen
(1) STP (Standard temperature and pressure): 273 K, 101325 Pa. << | Content | >> |