
|
BRHS /
Structure of the reaction zone and flame temperature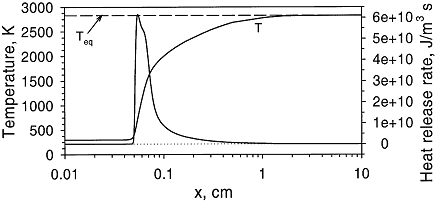 Figure 1. Distributions of temperature and heat-release rate in the \mathrm{H_2}-\mathrm{O_2} flame. From Liu, Guo, Smallwood & Gulder (2002) (LiuF:2002). The study of the laminar flame structure is of fundamental interest in combustion science. It is also a necessary first step towards understanding combustion processes. In turbulent combustion, for example, there are many occasions where chemical reactions are localised in laminar flames that are being wrinkled and perturbed by turbulence. While entire monographs have been devoted to detailed experimental studies of the structure (e.g Fristrom (1995) (FristromRM:1995)) there appears to be no focus on hydrogen combustion. Studies of the flame stucture are quite difficult as laminar flames are very thin and complex. 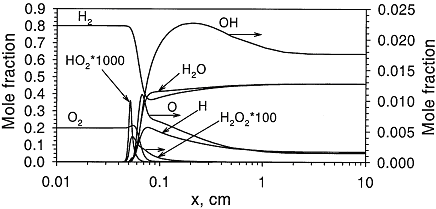 Figure 2. Distributions of mole fraction of species in the \mathrm{H_2}-\mathrm{O_2} flame. From Liu, Guo, Smallwood & Gulder (2002) (LiuF:2002). The internal flame structure is known to depend on the chemical kinetics of the combustion reactions, and, thermodynamic as well as transport properties of all species in the flame. Solutions of the conservation equations of mass, energy and chemical species by means of numerical codes (e.g. Kee, Rupley & Miller (1987) (KeeRJ:1987) and Kee, Rupley & Miller (1989) (KeeRJ:1989)) are being used to resolve the details of the flame structure. The thermo-chemical and transport properties of the species are included via databases into the codes. The reaction mechanisms used in the simulations are taken from separate studies. An example of results obtained in this way is given by Figure 1 and Figure 2, showing distributions of temperature, heat release and species concentrations in a rich \mathrm{H_2}-\mathrm{O_2} premixed flame with an equivalence ratio of 2 at atmospheric conditions (after Liu, Guo, Smallwood & Gulder (2002) (LiuF:2002)). A characteristic feature of the heat release in the flame is its sudden start caused by the chain branching reaction \mathrm{O} + \mathrm{H_2} \rightarrow \mathrm{H} + \mathrm{OH}
initiated by the rate limiting reaction \mathrm{H} + \mathrm{O_2} \rightarrow \mathrm{O} + \mathrm{OH}
having an activation energy of about 17 kcal/mole. Very quickly after the start of the chain branching reactions a high concentration of radicals is reached within the flame followed by a slow and extended, three molecular radical recombination zone where reactions like \mathrm{H} + \mathrm{OH} + \mathrm{M} \rightarrow \mathrm{H_2O} + \mathrm{M}
\mathrm{H} + \mathrm{H} + \mathrm{M} \rightarrow \mathrm{H_2} + \mathrm{M}
\mathrm{O} + \mathrm{O} + \mathrm{M} \rightarrow \mathrm{O_2} + \mathrm{M} \quad \text{etc.}
lead to final equilibrium. The heat relase during the conversion from reactants to products causes the temperature to rise (see Figure 3). 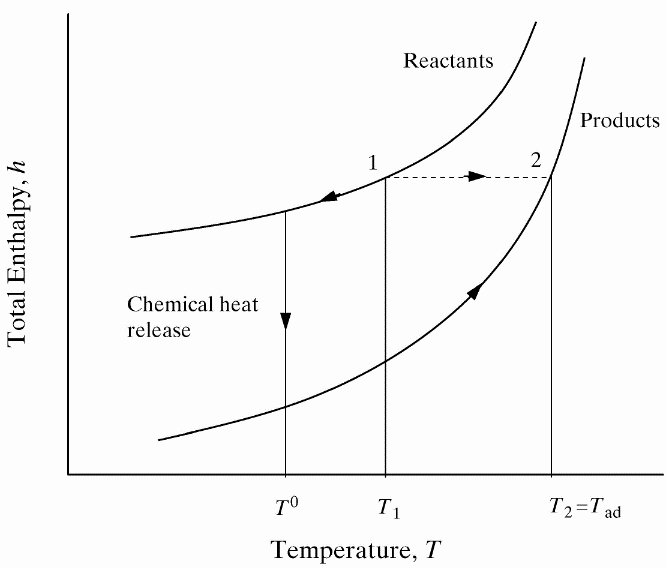 Figure 3. The principle of energy conservation during the conversion of reactants into products during combustion. From Law (2006) (LawCK:2006a). In the absence of heat losses to the surroundings, the final temperature attained is called the adiabatic flame temperature, T_f^{\scriptsize \text{ad}} (see Figure 3). More specifically, if a given uniform mixture with an initial temperature and composition is made to approach chemical equilibrium through an adiabatic, isobaric process at pressure P, then the final temperature is called the adiabatic flame temperature, T_f^{\scriptsize \text{ad}} (see page 37 of Law (2006) (LawCK:2006a)). When an adiabatic combustion process is isochoric instead of isobaric, i.e. when the volume occupied by the product mixture equals that of the reactant mixture prior to combustion, the final flame temperature T_f^{\scriptsize \text{ad,cv}} is larger than T_f^{\scriptsize \text{ad}}. The larger value of T_f^{\scriptsize \text{ad,cv}} stems from the fact that no work is done on the surroundings during isochoric combustion. All energy released by the chemical reactions is invested in raising the temperature of the mixture. Conversely, during isobaric combustion the hot product gases have to displace the surrounding air for the pressure to remain constant. A portion of the energy released by the chemical reactions that is consumed to displace the surroundings becomes unavailable for heating the mixture. 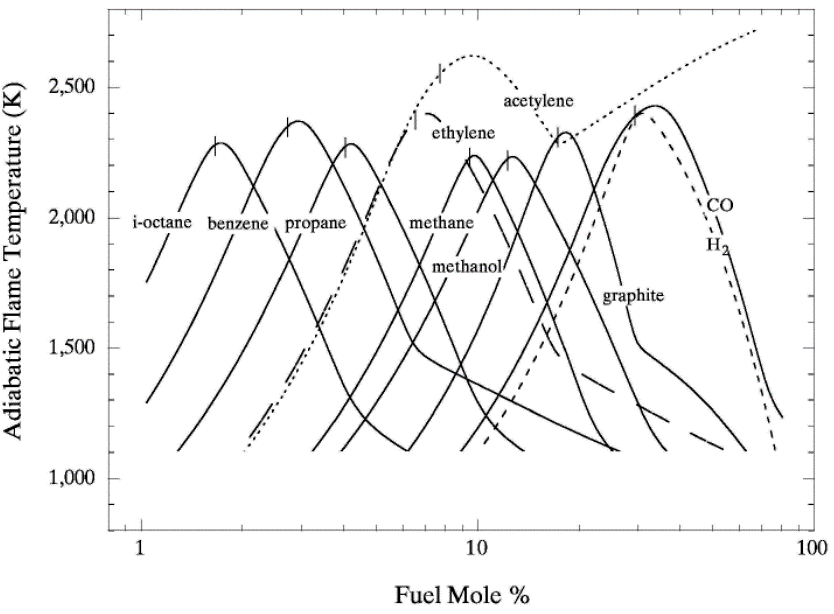 Figure 4. Adiabatic flame temperature, T_f^{\scriptsize \text{ad}}, as a function of the mole percent of fuel for several fuel–air mixtures at initial conditions of 1 bar and 298.15 K. The vertical bars indicate stoichiometric concentrations. From Law (2006) (LawCK:2006a). Figure 4 illustrates the behaviour of the adiabatic flame temperature, T_f^{\scriptsize \text{ad}}, as a function of mixture composition for a variety of fuels mixed with air. With all fuels the following trend is observed: the adiabatic flame temperature attains a maximum at a fuel concentration slightly above the stochiometric value, and levels off as the fuel concentration approaches the flammability limits. When T_f^{\scriptsize \text{ad}} is plotted against the fuel concentration, the locations of the flame temperature curves are seen to be scattered along the the horizontal axis. However, when these curves are plotted against the equivalence ratio, as is done in Figure 5, their apearance becomes more systematic because the stoichiometric concentration of all fuels coincide at \phi=1. The flame temperature curves are also seen to behave in a manner that allows them to be expressed by matematical relationships as a function of the equivalence ratio \phi=1. For fuel-lean mixtures at moderate pressures and temperatures of up to 2300 - 2400 K, the dissociation of product species is negligible and the product composition can be estimated from the overall chemical equation. This makes the calcualtion of the adiabatic flame temperature easier. Furthermore, the adiabatic flame temperature can approximated by simple formulas like the one developed by Chang & Rhee (1983) (ChangSL:1983) in the form: T_f^{\scriptsize \text{ad}} =a\cdot \left[1+b\cdot \mathrm{ln} \phi +c\cdot \left(\mathrm{ln} \phi \right)^{2} \right]
where
In the above expressions P, \phi and m respectively denote the pressure, equivalence ratio and mass. The coefficients for hydrogen-air mixtures are: a_{1} =2412.2 K; a_{2} = 17.9 K; b_{1} = 0.473 K; b_{2} = 0.021 K; c_{1} = 0.0217 K; and c_{2} = 0.0191 K. 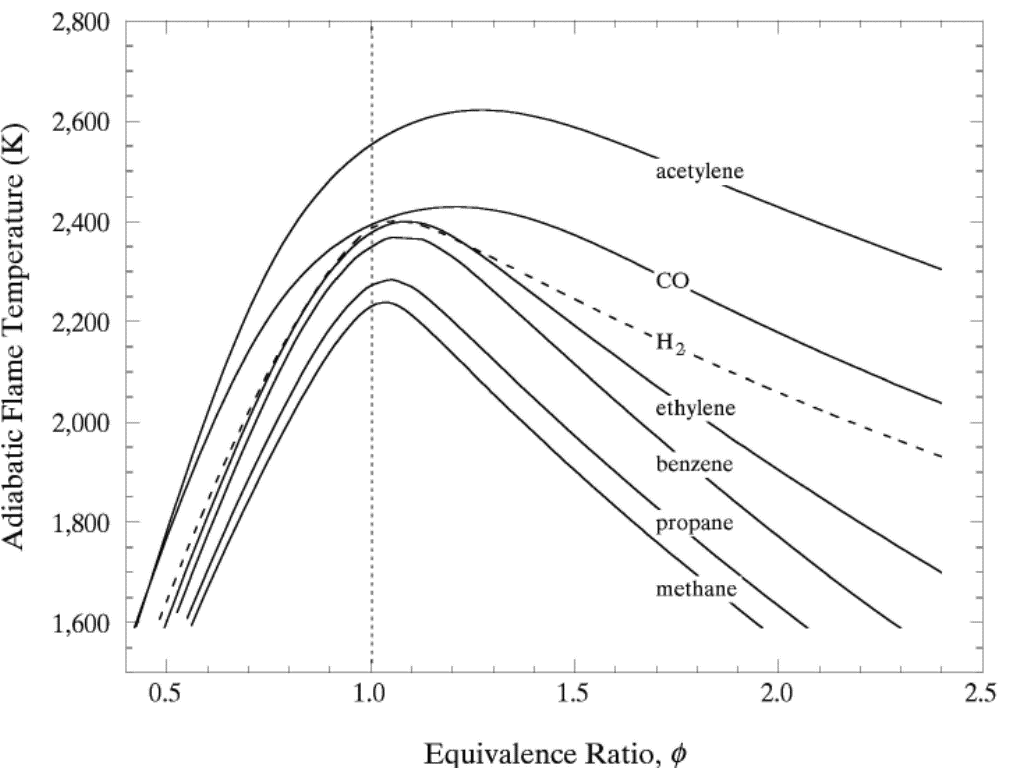 Figure 5. Adiabatic flame temperature, T_f^{\scriptsize \text{ad}}, as a function of fuel equivalence ratio, \phi, for several fuel–air mixtures at initial conditions of 1 bar and 298.15 K. From Law (2006) (LawCK:2006a). At higher pressure and temperature, and, with rich mixtures, the product mixture contains many more species because of dissociation. The composition of the products can then only be estimated by large reaction sets. Specialised chemical equilibrium codes then become a necessity to compute the adiabatic flame temperature. Bibliography Chang S.L. and Rhee K.T. (1983) Adiabatic flame temperature estimates of lean fuel/air mixture. Combustion Science and Technology, 35:203-206.(BibTeX) << Contributing Authors | Content | Laminar burning velocity and laminar flame thickness >> |