
|
BRHS /
Chemical Properties Of HydrogenHydrogen reacts both with non-metals (high electro-negativity) and with metals (low electro-negativity) to form either ionic or covalent hydrides (e.g., HCl, H2O). The electro-negativity, a measure for the attraction of electrons to the nucleus, of hydrogen is 2.20 (Pauling scale). Hydrogen is able to react chemically with most other elements. In connection with oxygen, hydrogen is highly flammable over a wide range of concentrations. As a fuel it represents a clean, environmentally benign energy source. The mass-related energy density of hydrogen is very high; 1 kg of hydrogen contains 132.5 MJ, which is approximately 2.5 times more energy than is contained in 1 kg of natural gas. The energy content of hydrogen is given as either lower heating value (LHV) of 242 kJ/mol or as higher heating value (HHV) of 286 kJ/mol. The difference of 15.6 %, which is large compared to other gases, is due to the heat liberated upon condensation of the water vapour (which could be captured in a turbine, but not in a fuel cell). A stoichiometric hydrogen-air mixture, where all fuel is consumed upon reaction, i.e., where maximum combustion energy is released, contains 29.5 vol% of hydrogen. The combustion product of hydrogen is water vapour. It burns in a non-luminous, almost invisible pale blue, hot flame to water vapour liberating the chemically bound energy as heat (gross heat of combustion). The flame temperature of a burning (premixed stoichiometric) hydrogen-air mixture is max. 2403 K. There is a wide flammability range of hydrogen (at room temperature) between 4 and 75 vol% of concentration in air and up to 95 vol% in oxygen. The lower flammability limit (LFL) as the minimum amount of fuel that supports combustion, is usually the “more important” limit, since it will be reached first in a continuous leakage. The flammability range widens with higher temperatures. The influence of the temperature is expressed in the modified Burgess-Wheeler equation for the LFL, which is for hydrogen (at ambient pressure) (ZabetakisMG:1967):
where ΔHc is the net heat of combustion and T given in [K]. The respective equation for the upper flammability limit (UFL) is (EichertH:1992):
valid for the temperature range 150-300 K. Measurements of upward flame propagation at higher temperatures (GasseA:1992) have shown a further increase of the UFL with initial temperature reaching 87.6 % at 673 K. There is still no experimental data available on the influence of moisture on the flammability limits. For the determination of LFL and UFL of mixtures of fuels, the Le Chatelier rule is the most commonly applied method:
where yi is the volume fraction and Li the flammability limit of fuel i. Le Chatelier’s rule was found to be in accurate agreement with experimental data for the system H2-CO, but shows deviations up to 35 % for the systems methane-propane or methane-ethane (SubramanyaM:2005). The GEXCON handbook states that "the formula does not work properly for H2". The potential for an explosion of a flammable hydrogen-air mixture is very high. The auto-ignition temperature, which is the minimum temperature of a hot surface that can ignite a flammable mixture, is for hydrogen in the range of 800-1000 K depending on the experimental conditions. It is relatively high, but can be lowered by catalytic surfaces. Hydrogen gas does not have a flash point as it is already a gas at ambient conditions. It means that cryogenic hydrogen will flash at all temperatures above its boiling point of 20 K. The minimum ignition energy, i.e., the spark energy required to ignite the "most easily ignitable hydrogen concentration in air" (which is usually not the stoichiometric mixture), is with 0.02 mJ very low, much lower than for hydrocarbon-air mixtures. A weak spark or the electrostatic discharge by a flow of pressurized H2 gas or by a person (~ 10 mJ) would suffice for an ignition. This is, however, no different from other burnable gases. The minimum ignition energy is further decreasing with increasing temperature, pressure, or oxygen contents. The hot air jet ignition temperature is lowest for hydrogen compared to all hydrocarbons decreasing further with increasing jet diameter. It is also dependent on jet velocity and mixture composition. The "maximum experimental safe gap" (MESG) is the maximum distance between two flat plates which still allows flame propagation through the gap; it is for hydrogen 0.08 mm. The “quenching gap” in air is the distance between two flat plates at which ignition of a flammable mixture is suppressed. It corresponds to the smallest diameter of a tube through which a flame can propagate. Faster burning gases have smaller quenching gaps. Hydrogen has a quenching gap of 0.64 mm. Because of the high explosion pressures, the MESG is always smaller than the quenching gap. 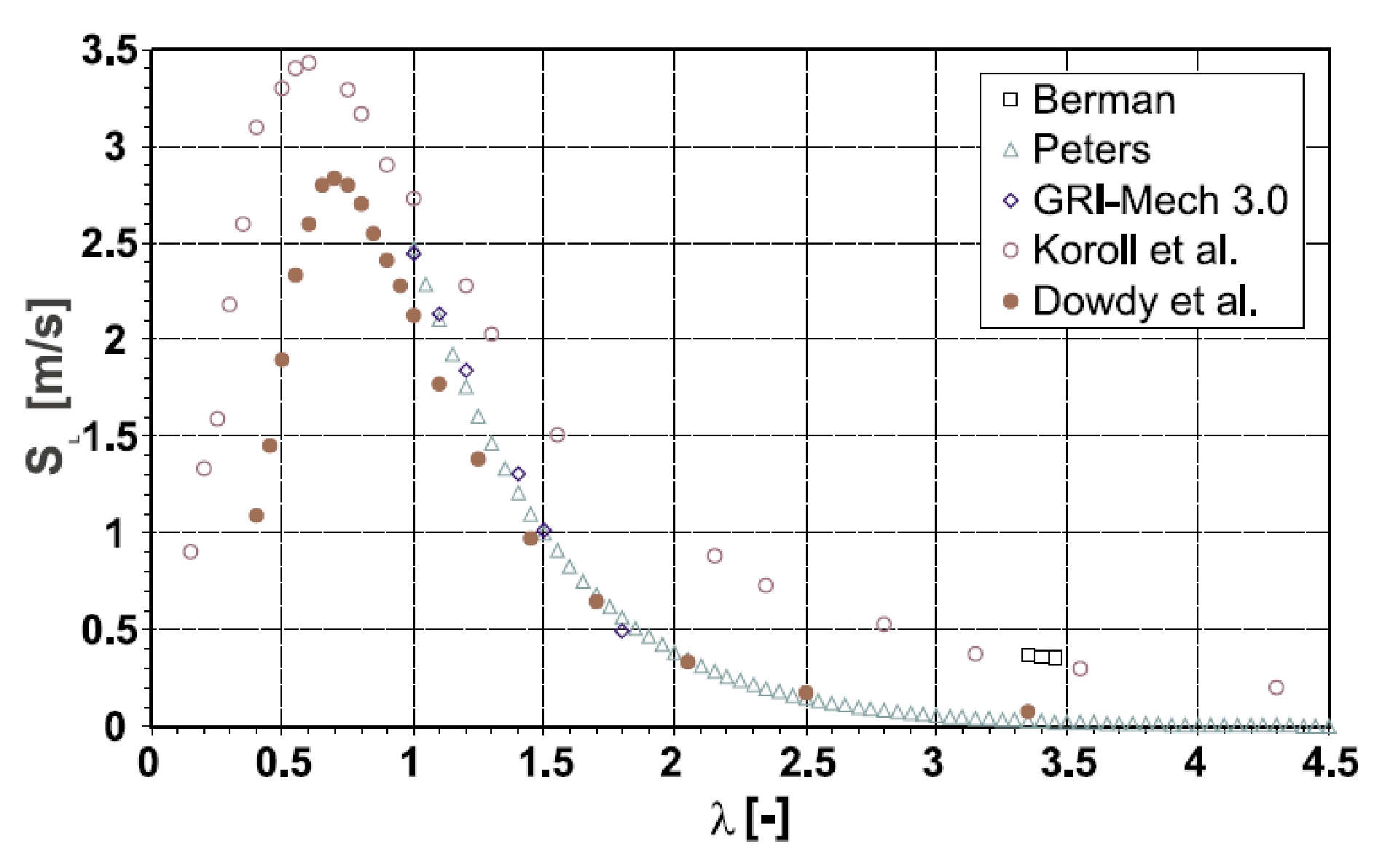 Fig. 1: Burning velocities in hydrogen-air mixtures as measured by various authors ([[http://www.hysafe.net/wiki/BRHS/ChemicalPropertiesOfHydrogen?action=bibentry&bibfile=DB&bibref=KroenerM:2002 | KroenerM:2002)]] The burning velocity in a flammable gas mixture, different from the flame speed, is indicating the speed with which a smooth plane combustion wave advances into a stationary flammable mixture and is a pertinent property of the gas depending on temperature, pressure, and concentration. The burning velocity of hydrogen in air at stoichiometric ambient conditions (Fig. 1) is 2.55 m/s reaching a maximum of 3.2 m/s at a concentration of 40.1 %, which would even increase to 11.75 m/s in pure oxygen. Compared to other hydrocarbon fuel-air mixtures, it is highest for hydrogen because of its fast chemical kinetics and high diffusivity. The higher the burning velocity, the greater is the chance for a transition from deflagration to detonation (DDT). In contrast, the flame speed, which is related to a fixed observer, is much greater than the burning velocity due to the expansion of the combustion products, instabilities, and turbulent deformation of the flame. The maximum possible speed of a deflagrative burning flame is given by the speed of sound in the combustion products gas mixture, which is 975 m/s for a stoichiometric hydrogen-air mixture. The detonability range is usually given to be 18-59 vol% of hydrogen concentration, however, the range was found to be depending on the system size. In Tieszen et al. (TieszenSR:1986), a detonation range of 13-70 % of H2 is given for a 43 cm tube. In the Russian detonation test facility RUT, the largest of its kind, a lower detonability limit of as low as 12.5 vol% has been observed. In pure oxygen, the detonation range is extended to 15-90% (ZabetakisMG:1967). The detonation velocity in air reaches values in the range of 2000 m/s; in pure oxygen, it is up to 3500 m/s. The size of the detonation cell is a measure of the reactivity; the smaller the cell, the more reactive is the mixture (Fig. 2). It serves to some extent as an indicator for DDT and can be measured experimentally. A stoichiometric hydrogen-air mixture with a cell size of 15 mm is highly reactive, whereas a stoichiometric methane-air mixture with a cell size measured of approx. 330 mm is the least sensitive of the common fuels. Cell sizes increase with increasing deviation from stoichiometry. It was in the late 1970s, when the usefulness of measurements of the detonation cell size λ was well acknowledged. First step was finding a correlation between cell size and critical tube diameter (d=13*λ). This empirical law was the basis to develop a simple surface energy model which allows the derivation of a critical initiation charge weight for various hydrocarbon-air mixtures in pretty good agreement with experimental data. The critical tube diameter is the minimum diameter required for a detonation wave to emerge from a tube and become a detonation in an unconfined cloud. It is a measure of minimum dimensions of an unconfined detonable cloud. The detonation initiation energy given in mass of high explosive (TNT or tetryl) is the minimum energy necessary to initiate a spherical detonation wave; the energy content of tetryl corresponds to 4.3 MJ/kg. The distance in which the flame front at the ignition point develops to a detonation depends on many parameters such as temperature, pressure, mixture composition, geometry (obstacles), and ignition source strength. For a stoichiometric hydrogen-air mixture to detonate, a typical figure of tube length over diameter ratio is approximately 100. It is known from the experience that a hydrogen-air gas cloud evolving from the inadvertent release of hydrogen upon the failure of a storage tank or pipeline liberates only a small portion of its thermal energy contents in case of an explosion, which is in the range of 0.1-10 %, in most cases < 1 % (LindCD:1975). 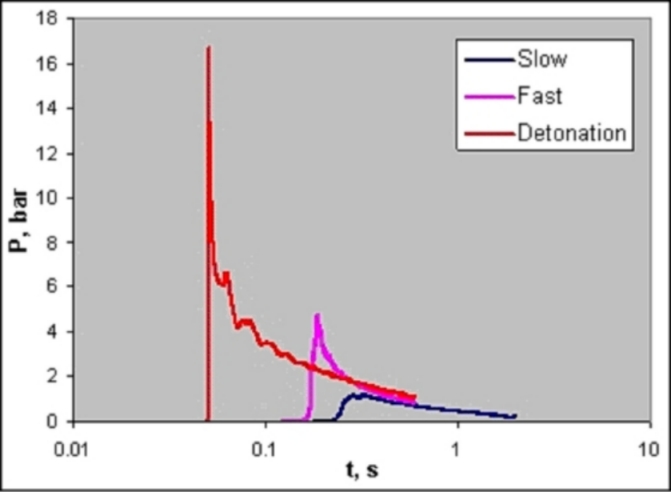 Fig. 3: Pressure signals from different hydrogen combustion modes ([[http://www.hysafe.net/wiki/BRHS/ChemicalPropertiesOfHydrogen?action=bibentry&bibfile=DB&bibref=KuznetsovM:2005 | KuznetsovM:2005)]] The explosion of a hydrogen-air mixture cloud results in the formation of a pressure wave, which is different dependent on the combustion mode as is shown in Fig. 3. In the deflagration of a free hydrogen-air gas cloud, the maximum overpressure is in the order of 10 kPa. An overpressure of 7 kPa is still deemed not dangerous; at 7 kPa, people would fall down to the ground; at 35 kPa, damage of ear drums is expected; 240 kPa is considered a threshold value above which fatalities must be taken into account. The thermal energy radiated from a flame corresponds to the higher heating value. It can be reduced due to absorption by moisture in the atmosphere. The radiation emitted from a hydrogen flame is very low due to a strong absorption by the ambient water vapour (emissivity ε < 0.1) unlike hydrocarbon flames (ε ~ 1) (ArthurDLittle:1960). Therefore, despite its high flame temperature, the burning hazard is comparatively small. The major problem is given in the non-visibility even in a dark room (unless impurities in the air are present), and therefore difficult to recognize and localize. An advantage of hydrogen-air fires is the fact that there is no smoke generation (assuming no other material be ignited), which is important for confined areas. Invalid BibTex Entry! << Physical Properties of Hydrogen | Content | Main Characteristic Data of Hydrogen >> |