|
BRHS /
Methods to Determine Structural ResponsesForces acting on a structure will lead to a deformation to an extend which depends on the material properties and structure composition. For a static or quasi-static load, i.e., a constant or slowly changing load like from a simple deflagration, it will be in equilibrium with the internal forces resulting in a deformation of the structure. For a dynamic load, i.e., a fast load transient, however, a “dynamic” contribution from inertia forces will add to the equilibrium, which can show positive or negative acceleration, i.e., mass and stiffness of the structure will play a major role. The load from a gas explosion is considered a dynamic load due to its short overpressure duration, which is typically in the range of 100-200 ms. Detonations tend to excite the high natural frequencies of a building, whereas deflagrations are more effective for the lower frequencies. It appears to be technically more difficult to design a building against both explosion modes rather than only one. Methods used in order to determine structural response and resistance belong to three main categories:
Empirical Methodsa) Methods Based on Pressure Peak Values 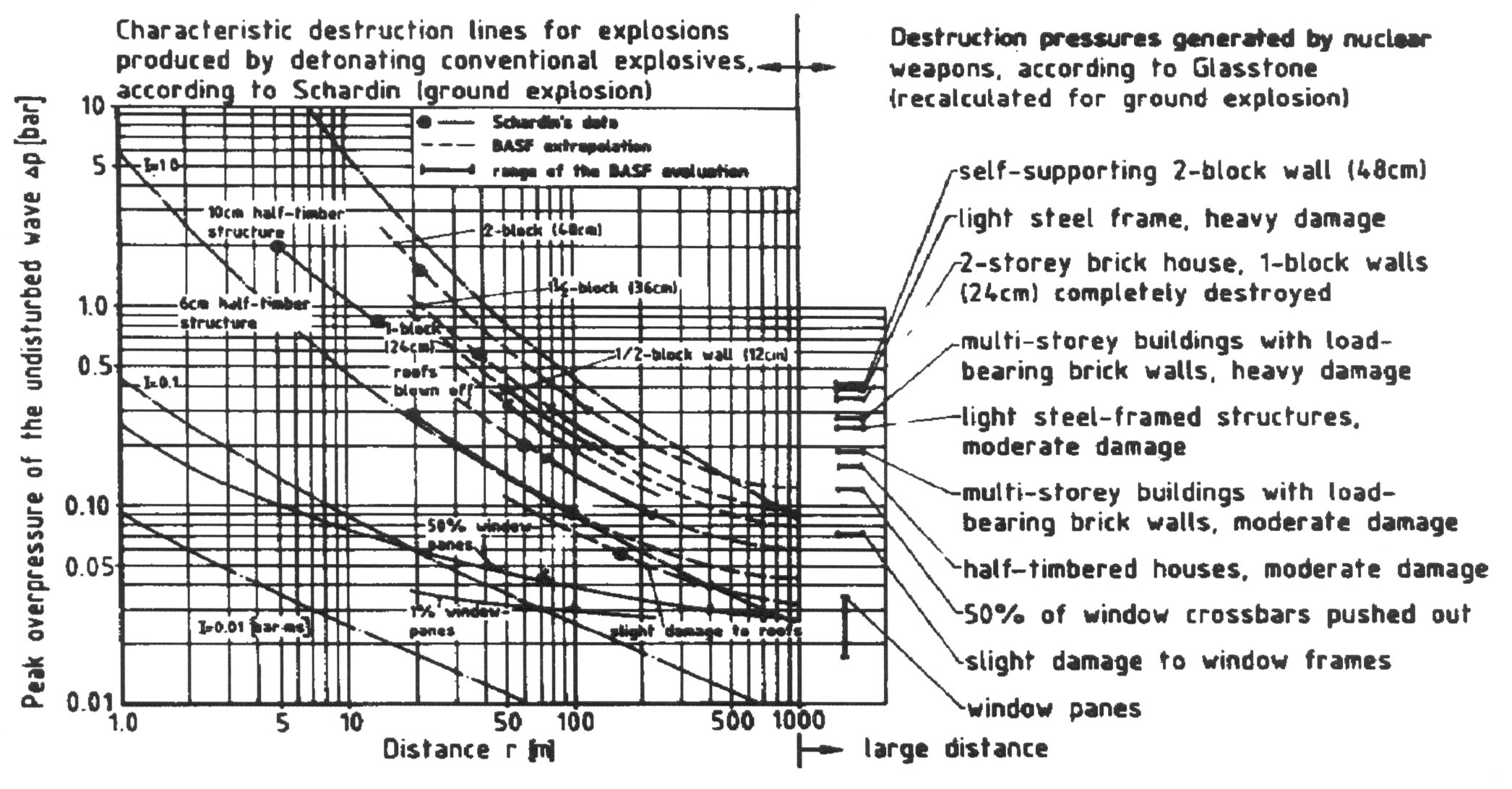An empirical and very global approach of determining the strength of structures is to relate overpressures to the degree of observed damage. This very useful and easy handling method is widely used. The relationship between pressure and damage, which is derived from TNT explosions, cannot satisfactorily be transferred to vapor cloud explosions. The pressure decay from a TNT explosion is much faster than from a vapor cloud explosion. The high impulse and the suction effect due to the below-atmospheric pressure phase will certainly result in a different damage pattern. Thus damage criteria such as those derived by Schardin (see Fig. 1) from TNT explosions are not directly applicable (GiesbrechtH:1988). Many pressure criteria were defined in the past related to various structures and specific components, however, varying over a large uncertainty range. A rough classification is given in Table 1. Table 1: Damage classification (CPR16E:2005:GreenBook)
A pressure peak for domino effect really useful for risk assessment may also be defined at a value of 20 kPa (MEDD:2004). b) Methods based on P-I diagrams 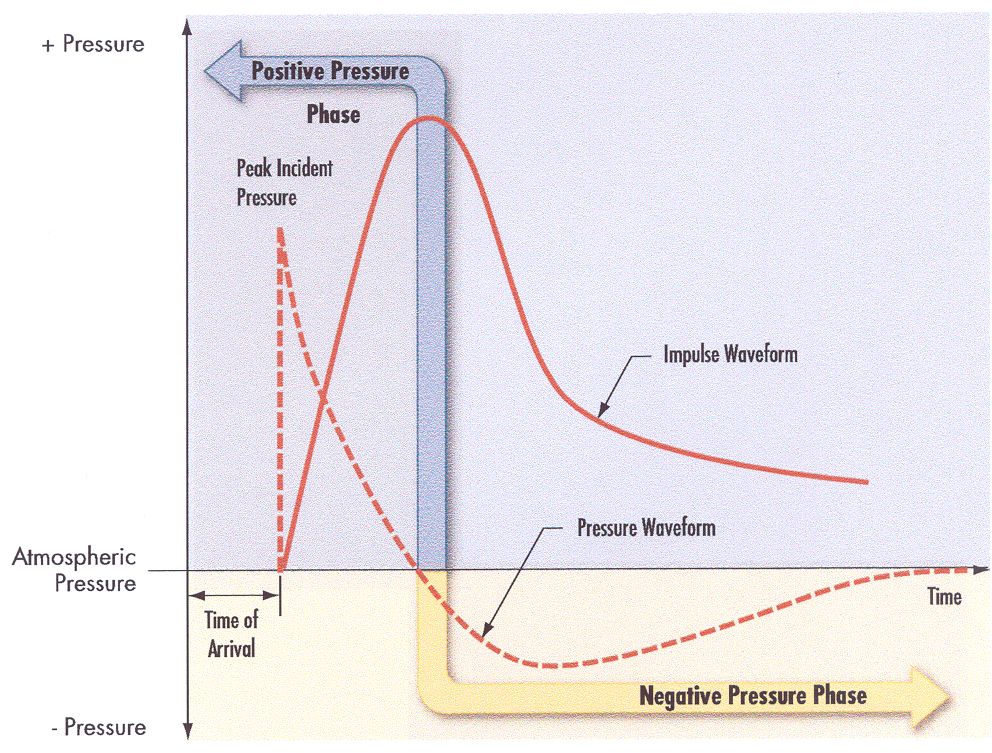Another global approach may couple pressure peak with impulse. The impulse, i.e., the pressure – negative and positive – integrated over time, is a measure for the explosion energy (Fig. 2), which also varies in time and space over the exposed structure surface. Damage to the structure resulting from a blast wave may be subdivided into direct effects and what is named “progressive collapse”, a kind of secondary failure following the change of the load pattern on a structure due to the direct effects. Features of a P-I diagram are the asymptotes in P and I direction and the monotonic relation between P and I, which suggests a subdivision into three regimes: impulse-controlled, peak load-controlled, and an intermediate dynamic stage (LiQM:2002). P-I diagrams are being widely used in damage assessments not only for structural damage, but also for predicting blast-induced human injuries. They are providing useful information on the vulnerability of targets. 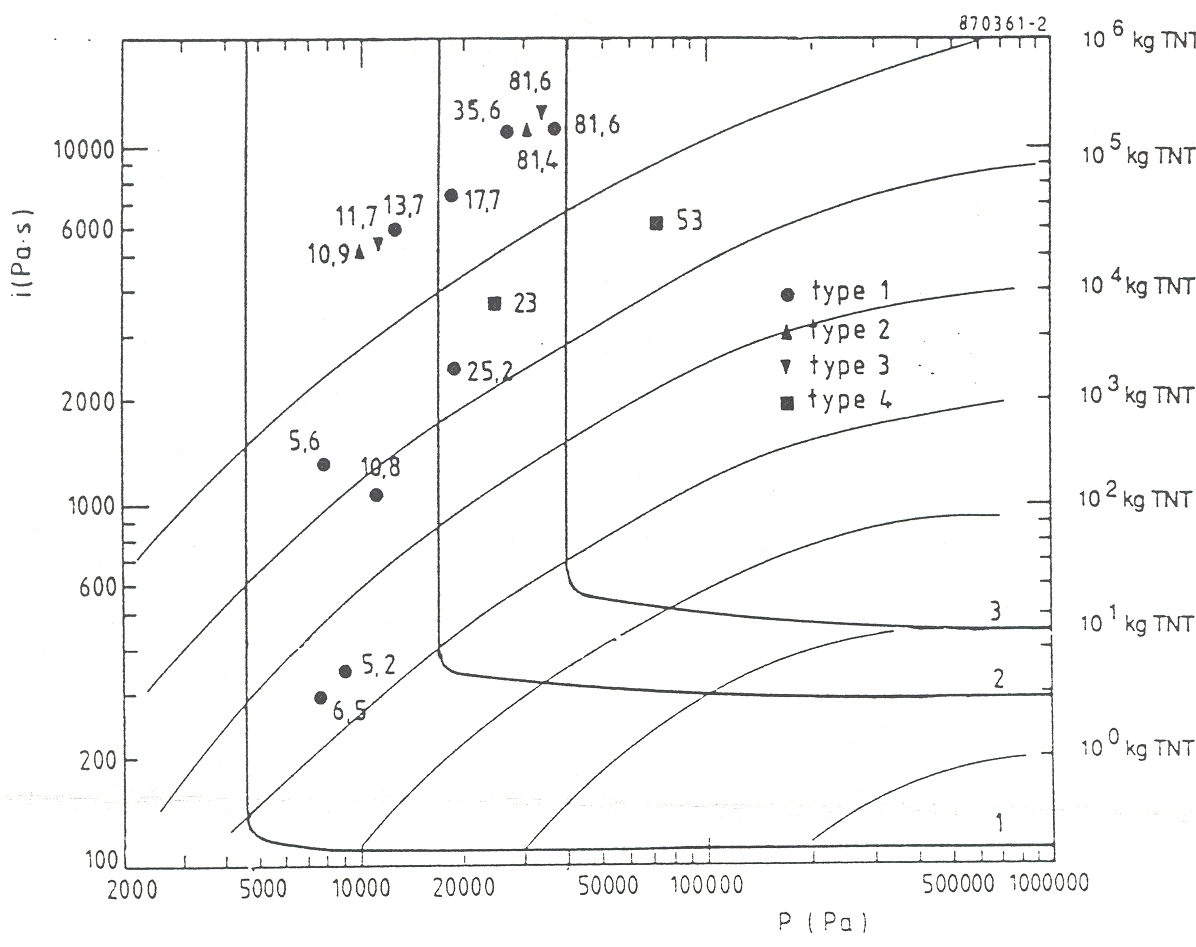Damage levels can also be visualized in pressure-impulse diagrams, where different regions can be defined by iso-lines. An example is given in Fig. 3 showing the experimental results for the observed damage in per cent, after different types of houses were exposed to a certain explosion (pressure/impulse) load (CPR16E:2005:GreenBook). Important for the damage effect of a short-term load (= shock wave) is only the impulse, whereas it is the maximum overpressure for that of the longer-term load (= pressure wave). The solid lines in the figure indicate the lower boundaries for light damages, for severe damages, and for collapsing structures of the houses investigated. The estimation of the level of damage is usually done taking either fixed-limits methods or the PROBIT method. In a fixed-limits method, the hazard level is compared to fixed limits like IDLH (Immediately Dangerous to Life or Health) values or pressure thresholds, as given in the literature. It is a simple method, but may lead to wrong conclusions in transient hazards. In such cases, the PROBIT method is the more appropriate one. First a hazard load, L, is estimated, which could be the overpressure in an explosion or the integrated thermal flux at a certain location. Then the PROBIT or probability unit, y, is given by y = k1 + k2*ln L, which can be related to a certain probability of death, injury, or damage. k1 and k2 are empirical parameters, which are specific to, e.g., toxic chemicals or fire and explosion effects and can taken also from the literature (CSCHE:2004). For the assessment of the probability to obtain a certain level of damage, so-called probit functions have been introduced and suitable damage criteria have been defined (CPR16E:2005:GreenBook). Computer simulation techniques have been developed by SRI International, USA, for analyzing hydrogen explosions and the subsequent response of structures and humans. The thermodynamic code TIGER is used to calculate explosion pressures and expansion characteristics, which are input to the DYNA3D model to determine the impact on structures. A simplification of the blast load damage analysis has led to the development of the pressure-impulse (PI) methodology which is based on the observation that for a broad range of structures, the final damage state depends on peak pressure (P) and total impulse intensity (I) only. This methodology allows for a quick and easy evaluation of accident scenarios by employing a continuously growing library of pressure-impulse load and damage curves that are based on either experimental data or computer simulations (Sanai 1996). Analytical MethodsA structure can be schematically represented by a system of masses coupled with springs or dampers. For the static case, if linear-elastic or non-linear-elastic forces are acting, displacements of the masses become zero again, when the load disappears. In case of plastic or elasto-plastic behavior, displacement is zero or very small, until the maximum load is reached. Under a static load, the structure will then fail; under dynamic load, it may retain a residual displacement. In general, structures must be designed to react elastically under typical loads like wind. Plastic displacement must be limited to abnormal load conditions. The maximum displacement depends on load duration, tD, and the natural frequency of the structure, T. For low tD/T ratios, the displacement is smaller than for static loads. For large tD/T ratios, the displacement can be larger than under static load conditions. Other important parameters are the static strength and the ductility. Load schemes are distinguished between a step function for a long-duration pressure wave and an impulse load for a short-impact shock wave. Detonations tend to excite the high natural frequencies of a building, whereas deflagrations are more effective for the lower frequencies. It appears to be technically more difficult to design a building against both explosion modes rather than only one. However for hydrogen explosions experience proves that detonations or strong deflagrations must be preferred. Several analytical procedures may be distinguished. They have to be coupled with structural engineering calculations. Still these methods are likely to lead to very conservative structural designs, and are rather suitable for hand calculations. A comparison between detonations of explosives and blast waves resulting from nuclear weapon explosions, characterized by quasi-static pressure due to a longer impulse time shows that, assuming the same damage, the detonation pressure or the pressure resistance of an object is much higher than the resistance against a blast wave from nuclear tests (PfortnerH:1975). The pressure resistance behavior of a building under detonative dynamic and quasi-static loading derived from numerous detonative explosion studies can be summarized in an empirical equation for the quasi-static reference overpressure of the building pst: pst = 0.15 * pr2/3, where pr is the perpendicularly reflected overpressure or the pressure resistance of the building subjected to a detonation. If the TNT equivalent, as derived from the damage of some of the severe accidents, is interpreted as the incident pressure wave in the order of 70 kPa, resulting from a deflagration, the respective quasi-static pressure would be with pst = 22 kPa much smaller. a) Dynamic Load Factor DLF The analytical procedure is usually simplified by introducing a so-called dynamic load factor (DLF), which is defined as the ratio of maximum dynamic displacement over static displacement. It transforms a dynamic peak load into a static load with the same effect on the structure. The DLF is dependent on the dynamic load time and the natural frequencies of the structure. For long explosion times and in case of an idealized triangle-shaped shock wave load, the DLF approaches its boundary limit of 2 (MEDD:1994). b) Single Degree-of-Freedom Model SDOF In a simple method, a static working load is assumed to simulate the effects of blast loads onto structures. This conservative approach, however, cannot predict structure performance and seems to be not optimal for transient blast loads. An improvement of modeling is given with the quasi-static methods which specify a triangular pressure pulse and determine the dynamic structural capacity as a function of the material strengths of the structure. The structural response can be found by using the charts. Single degree-of-freedom (SDOF) models analyze critical components in terms of their structural resistance and predict the response of the structure which then determines the damage level (USACE:1990)(USACE 1990). Numerical MethodsMore information is obtained from multi-degree-of-freedom (MDOF) models, sophisticated CFD models with the possibility to consider flame propagation and pressure profiles also from local explosions. Dynamic finite-element analyses with tools such as ADINA, LS-DYNA, AUTODYN, ABAQUS Explicit may provide the best judgement on whether or not a structure is able to withstand a blast wave. However, one must be very careful when using software which is still under development and which is still not fully validated to industrial applications. Numerical methods are also usually very sensitive to parameters and calculation grid changes. Invalid BibTex Entry! << Interaction of Blast Wave with Structure | Content | Flammability and Combustion Characteristics >> |
